

見てて飽きが来ない形体を目的としたときに、どのような造形が望ましいでしょうか。この問いに一般的な答えを導くことはほぼ不可能ですが、ある程度の仮説を持って制作を行う必要があります。また歴史のあるビジュアル・アートやデザインの中でも多くの議論がなされてきました。本記事では、いかに視覚的に好ましい(ずっと見てても飽きさせない)図像を体系的に得るかについて、一つの例を示したいと思います。
一般的に、造形を構成しようとしたときに、シンプルな調和を追求しすぎても、乱数を用いた不規則さのみに頼っても、どちらにしても凡庸な図像構成になってしまいます。逆説的に、ある程度の調和と、ある程度の無作為性が合わさったときに、視覚的におもしろい図像が生まれ得るのです。調和からの逸脱、複雑性の中に見出さられる規則性、相反する秩序と混沌が同居する瞬間、お互いがその特質を補完しあうことで好ましい結果を得られるということは、実際にプログラミングをしてみると経験的に理解できるはずです。
こうした、理にかなった(調和のとれた)複雑性は、Gary William Flakeの”The Computational Beauty of Nature: Computer Explorations of Fractals, Chaos, Complex Systems, and Adaptation”の中で“Effective Complexity”として紹介され、この概念はGenerative Artを広く定義したPhilip Galanterのテキストにも美的尺度(Aesthetic Measure: 美を判断する基準)として引用され批評の中でも機能しています。
本稿では、このEffective Complexityを最大化しうるような形を比較的簡単に再現でき、かつ応用展開が可能な方法論を紹介します。この造形プロセスは、規則性をデザインするプロセスと複雑性をデザインするプロセスに分けて考えられます。
規則性、均衡のデザイン
1)初期状態に幾何学プリミティブを利用する
形体をデザインする上で、最初に、シンプルな幾何学プリミティブの利用します。プラトン立体(正多面体)、球、トーラス、コーン、方形(Plane)、円、など基本的にCG描画ライブラリにデフォルトで呼び出し関数が組み込まれている形状を選びます。こうした図形は幾何学的な対称性を持ち、操作がしやすく応用が効くからです。また、球体や正多面体といった中心を持つ図像は最終的な出力において調和が容易に得られます。複雑な抽象図形として、正多面体をもとにした造形デザインは16世紀のWenzel Jamnitzerなどが歴史の中で観測され、おそらくその歴史はギリシア時代まで遡れます。
2)画面構成の構図的な最適化
調和のとれた構図を目指すという作業は、2次元平面的なバランスを考えることと捉えることができます。これは定量化することは難しいですが、対角線を用いた構図、景の多層化、中心点(消失点)の配置、二次元の形体の意識といったパターンなどが考えられますが、いずれにせよ、大局的には、一般的な構図選択が望ましいと言えます。

複雑さ、不規則性、細密さのデザイン
生物や物理現象の生成プロセスはしばしアルゴリズムとして近似でき、多くのCGデザインで利用されてきました。しかし、ここで紹介するのは、微分方程式などを使わずに理解できる、つまり、単純な回転・スケーリング・平行移動の静的なコピーのみによって再現できる方法を提案します。
それは、コピーを反復的(もしくは再帰的)に行うなかで、確率的なバリエーションを持たせるという方法です。この方法のみでも、視覚的デザインの潜在的な可能性がまだまだあると言えます。
※コードはopenFrameworksとglmの記法を用いています。
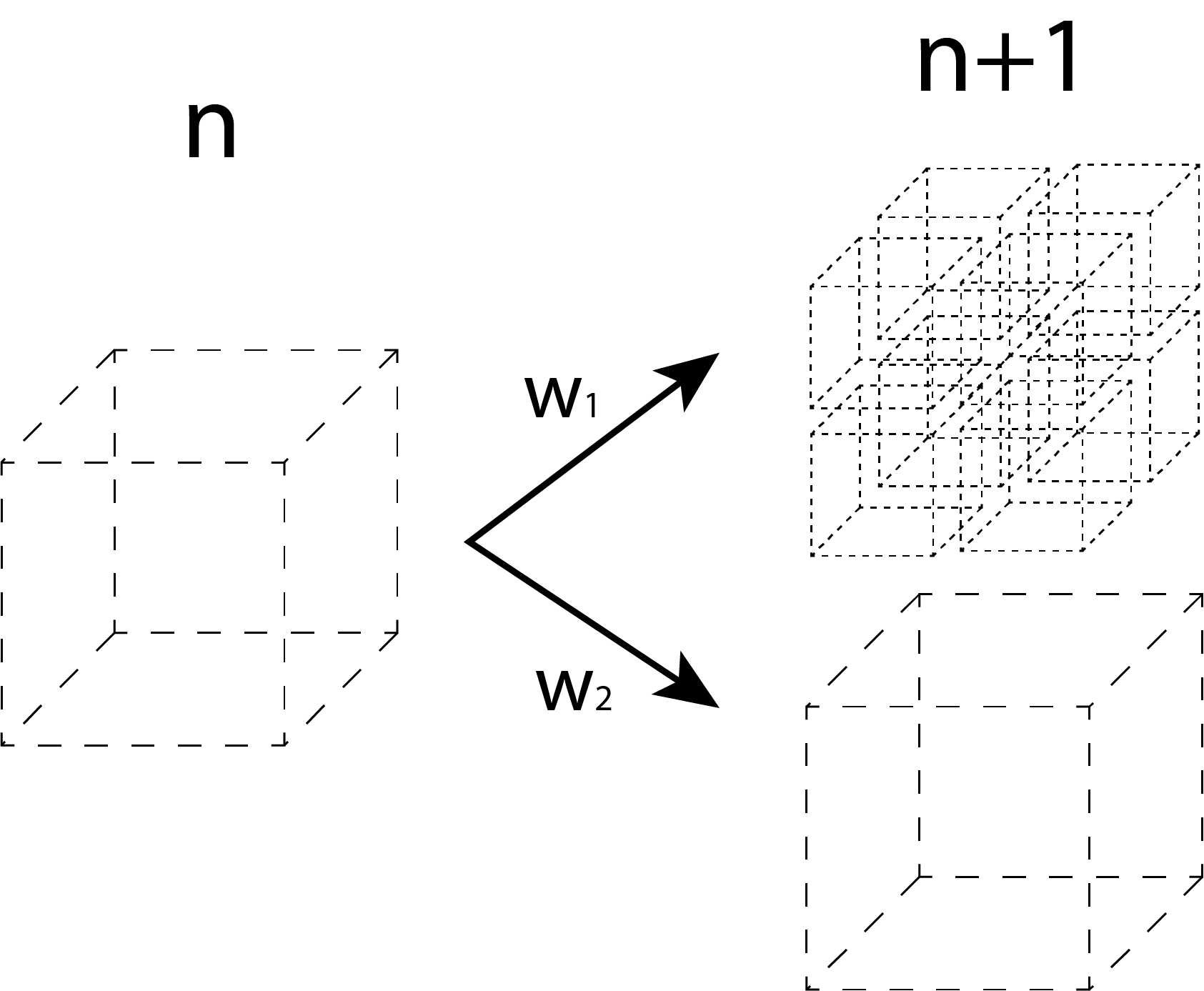
1)細分化/変換コピーの確率的バリエーション
変換の仕方を確率的に決定します。例えば、二分の一にスケーリングしてコピーしたり、回転をしてコピーしたりします。この時の状態、つまりモデル・マトリックスを保持したまま、次のステップの細分化/変換を行います。こうした操作を確率によってバリエーションを持たせます。
行列をグローバルのスタックに保持したり取り出すのは面倒なので、関数の引数に行列を渡し、都度計算に利用するようにするとシンプルになります。
|
1 2 3 4 5 6 7 8 9 10 11 12 |
void structure(const mat4& _m){ mat4 m = _m * rotate(-90, vec3(0,0,1)); // z軸に-90度回転する float coin = ofRandom(1.); // 確率で分岐 if (coin < .5) { tower(m); // 別の変換関数を呼び出す。モデル行列を引き渡す } else { pipe(m); // 別の変換関数を呼び出す。モデル行列を引き渡す } } } |
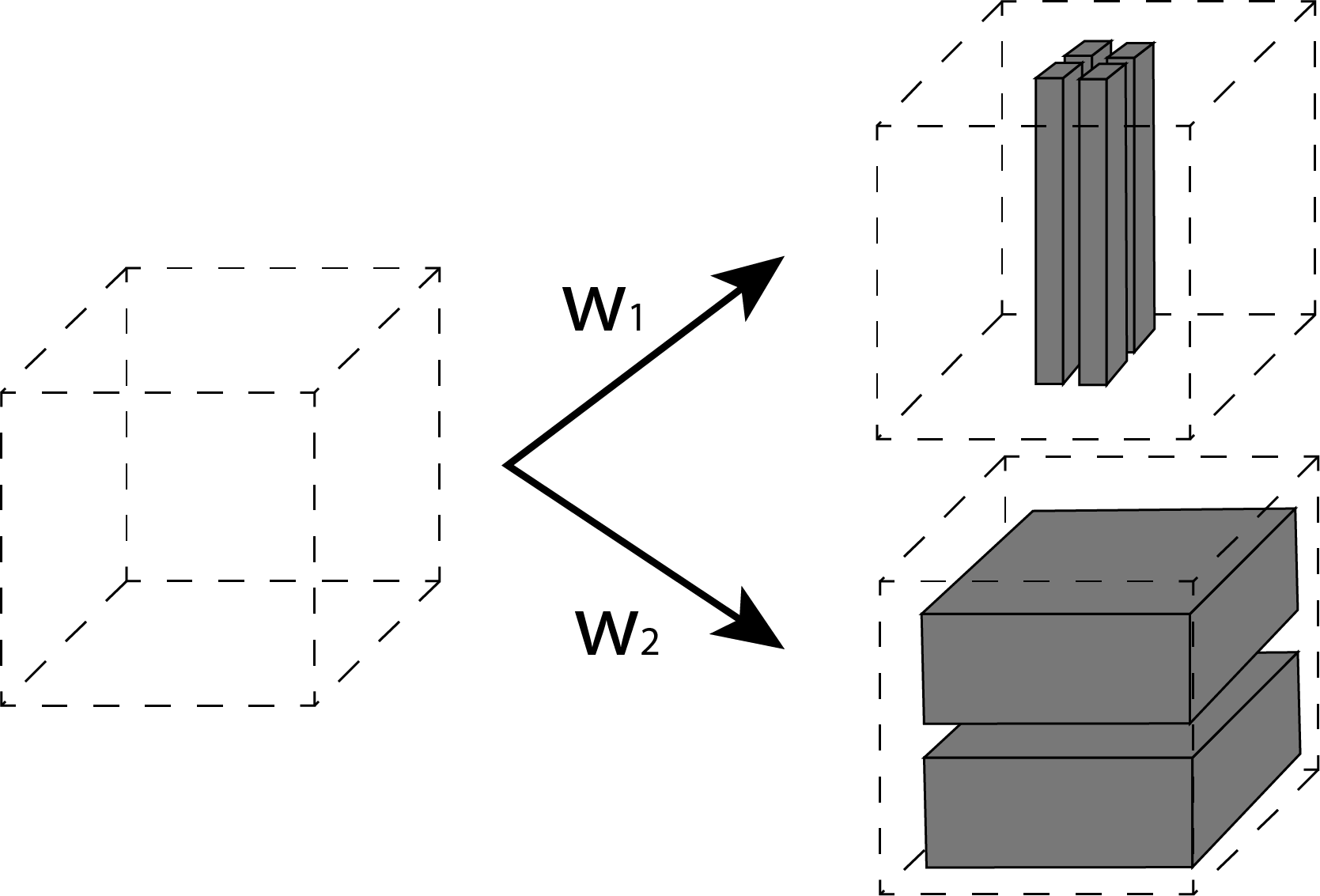
2)コンポーネントのデザインの確率的バリエーション
最終的な形体、頂点座標、面を出力する際もプラトン立体を使います。中でも立方体はxyz軸に対して直感的な変換操作が効くために利用しやすいです。ここでは、直方体を様々に組み合わせコンポーネントを構成します。例えば、柱や壁など。こうしたコンポーネントにあわせて関数名をつくると後に再利用も利きます。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 |
void beam(const mat4& _m){ ofFloatColor c(1.); ofFloatColor bc(0.1); mat4 m(_m); if (ofRandom(1.) < 0.5) { m = m * rotate(90, vec3(0,1,0)); } // 様々な種類のBoxを組み合わせる // 行列に対して平行移動やスケーリングをする m = _m; m = m * translate(vec3(0, 0, -0.05)); m = m * scale(vec3(0.06, 1, 0.02)); addBox(m, c); m = _m; m = translate(vec3(0, 0, 0.05)); m = scale(vec3(0.06, 1, 0.02)); addBox(m, c); m = _m; m = m * translate(vec3(0, 0.5, 0)); m = m * scale(vec3(0.06, 0.01, 0.1)); addBox(m, c); m = _m; m = m * translate(vec3(-0.05, 0, 0)); m = m * scale(vec3(0.02, 0.4, 0.1)); addBox(m, c); m = _m; m = m * translate(vec3(0.05, 0, 0)); m = m * scale(0.02, 0.4, 0.1); addBox(m, c); }; void addBox(const mat4& _m, const ofFloatColor& _c){ // ofVboMesh meshに頂点をappendしていく // ここで始めて頂点座標に、渡ってきた変換行列を乗算する ofMesh box = ofMesh::box(1,1,1, 1,1,1); for (int i = 0; i < box.getNumVertices(); i++) { vec3 v = _m * box.getVertex(i); vec3 n = transpose(inverse(_m)) * box.getNormal(i); // 法線の変換 box.setVertex(i, v); box.setNormal(i, n); box.addColor(_c); } mesh.append(box); }; |
最終的なSource Codeは以下になります。